En
lógica(
matemática), la
lógica proposicional es un
sistema formal diseñado para analizar ciertos tipos de
argumentos. En lógica proposicional, las fórmulas representan
proposiciones y las conectivas lógicas son
operaciones sobre dichas fórmulas, capaces de formar otras fórmulas de mayor complejidad.
[1] Como otros sistemas lógicos, la lógica proposicional intenta esclarecer nuestra comprensión de la noción de
consecuencia lógica para el rango de argume:ntos que analiza
Negación
La
negación es un
mecanismo de defensa que consiste en enfrentarse a los conflictos negando su existencia o su relación o relevancia con el sujeto.
Se rechazan aquellos aspectos de la realidad que se consideran desagradables. El individuo se enfrenta a conflictos emocionales y amenazas de origen interno o externo negándose a reconocer algunos aspectos dolorosos de la realidad externa o de las experiencias subjetivas que son manifiestos para los demás. El término negación psicótica se emplea cuando hay una total afectación de la capacidad para captar la realidad. Ejemplo: Fumar provoca cáncer, pero la persona lo niega e incluso estima que es favorable para su salud porque le resulta placentero
Conjunción, palabra o conjunto de ellas que enlaza
proposiciones,
sintagmas o
palabras, como su etimología de origen latino explica: cum, ‘con’, y jungo, ‘juntar’; por lo tanto, ‘que enlaza o une con’. Constituye una de las clases de
nexos. No debe confundirse con los
marcadores del discurso.
En
lógica y matemáticas una
disyunción es un "enunciado con dos o más elementos optativos". Por ejemplo "Puedes leer este artículo o editarlo", es una disyunción con dos elementos, mientras que "Puedes leer este artículo, imprimirlo o editarlo" es una disyunción con tres elementos.
Nótese que en el lenguaje cotidiano el uso de la palabra "o" significa a veces "alguno, pero sólo uno", por ejemplo: "¿Vas a ir mañana a México o a España?". En lógica, a esto se le llama "
disyunción exclusiva" u "o exclusivo". Cuando se utiliza formalmente, "o", permite que uno o más de los elementos de la disyunción sean válidos, por lo cuál "o" es también llamado "disyunción inclusiva"
Plantilla:Rf.
Para dos entradas A y B, la
tabla de verdad de la función
disyuntiva es: también la disyucción,
, es cuando hay dos elementos en dos conjuntos que forman una propocicion:
Más generalmente la disyunción es una fórmula lógica que puede tener una o más literales separadas con "o". Una sola literal se considera una
disyunción degenerada.
Símbolo
El
símbolo matemático para la disyunción lógica varia en la literatura. Además de utilizar "o", el símbolo en forma de "v" ("∨") es comúnmente utilizado para la disyunción. Por ejemplo: "
A ∨
B" se lee como "
A o
B". Esta disyunción es falsa si ambas
A y
B son falsas a la vez. En todos los demás casos es verdadera.
Todas las expresiones siguientes son disyunciones:
A ∨
B
¬
A ∨
B
A ∨ ¬
B ∨ ¬
C ∨
D ∨ ¬
E
La noción equivalente en teoría de conjuntos es la
unión. Y el símbolo representativo es "
O" y "
V"
Asociatividad y Conmutatividad
Para más de dos elementos de entrada
o puede ser aplicada a los primeros dos, y el resultado obtenido operado con
o al siguiente elemento y así sucesivamente:
- (A o (B o C)) ⇔ ((A o B) o C)
Debido a que
o es
asociativo, el orden de las entradas no importa: el mismo resultado se obtiene sin importar la asociación que se haga.
El operador
xor es también
conmutativo y por consiguiente el orden de los operandos no importa:
- A or B ⇔ B or A
Operación con bits
La disyunción es utilizada a menudo para operaciones con bits. Por ejemplo:
Nótese que en ciencias computacionales el operador
o puede ser utilizado para llevar un
bit a 1 aplicando una operación
o entre el bit y un 1.
Unión
La
unión utilizada en
teoría de conjuntos se define en términos de la disyunción lógica:
x ∈
A ∪
B si y solo si (
x ∈
A) ∨ (
x ∈
B). Debido a esto, la disyunción lógica satisface muchas de las mismas identidades que la unión de la teoría de conjuntos, como la asociatividad, conmutatividad, distributividad y las
Leyes.
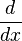, actúa sobre la función 
que se escribe a su derecha, produciendo una nueva función de 
:
